Adaptive, Model-based Monitoring for
Cyber Attack Detection
Alfonso Valdes, Keith Skinner, SRI International.
{valdes,skinner}@sdl.sri.com
Abstract
Inference methods for detecting attacks on information resources typically use signature analysis or statistical anomaly detection methods. The former have the advantage of attack specificity, but may not be able to generalize. The latter detect attacks probabilistically, allowing for generalization potential. However, they lack attack models and can potentially "learn" to consider an attack normal.
Herein, we present a high-performance, adaptive, model-based technique for attack detection, using Bayes net technology to analyze bursts of traffic. Attack classes are embodied as model hypotheses, which are adaptively reinforced. This approach has the attractive features of both signature based and statistical techniques: model specificity, adaptability, and generalization potential. Our initial prototype sensor examines TCP headers and communicates in IDIP, delivering a complementary inference technique to an IDS sensor suite. The inference technique is itself suitable for sensor correlation.
Keywords: Intrusion detection, Innovative approaches, IDS cooperation, Bayes nets.
Introduction
To date, two principal classes of inference techniques have been used in intrusion detection systems (IDS). In signature analysis
[1], descriptions of known attacks are encoded in the form of rules. Statistical systems [2, 3, 6] intend to "learn" normal behavior from data, and then issue alerts for suspected anomalies. Whatever inference techniques are used in IDS, they must typically meet stringent requirements of extremely high throughput and extremely low false alarm rate. In this paper we describe eBayes TCP, which applies Bayesian methods [4, 5] as an IDS inference technique.We have developed eBayes TCP as a component of the broad EMERALD system, which permits us to leverage from a substantial component infrastructure. Specifically, eBayes TCP is an analytical component that interfaces to the EMERALD ETCPGEN and EMONTCP components [
6]. ETCPGEN can process either live TCP traffic or TCPDUMP data in batch mode. EMONTCP extracts the TCP state for a number of generally simultaneous TCP connections. When we refer to "events", we mean events from EMONTCP, which already represents a considerable reduction from the raw TCP data.The innovation provided by eBayes TCP is that it captures the best features of signature-based intrusion detection as well as anomaly detection (as in EMERALD ESTAT). Like signature engines, it can embody attack models, but has the capability to adapt as systems evolve. Like probabilistic components, it has the potential to generalize to previously unseen classes of attacks. In addition, the system includes an adaptive capability, which can "grow" quite reasonable models from a random start.
EBayes TCP analyzes TCP sessions, which are temporally contiguous bursts of traffic from a given client IP. It is not very important for the system to demarcate sessions exactly. The analysis is done by Bayesian inference at periodic intervals in a session, where the interval is measured in number of events or elapsed time (inference is always done when the system believes that the session has ended). Between inference intervals, the system state is propagated according to a Markov model. After each inference, the system writes text and Intrusion Detection Internet Protocol (IDIP) alerts for sufficiently suspicious sessions.
EBayes TCP consists of two components: a TCP-specific module that interfaces to appropriate EMERALD components and manages TCP sessions, as well as a high-performance Bayesian inference class library. The latter has potential not simply to analyze a specific data stream, but also as a fusion engine considering heterogeneous sensors.
The remainder of this paper is organized as follows. We give a brief discussion of
Bayesian inference in trees, although the reader should refer to the bibliography for a more in-depth treatment. This is followed by a description of eBayes TCP itself, including the session concept, the TCP Bayes model structure, and the important nodes (measures) considered. After the eBayes definition, we present our innovative approaches to model adaptation and state transition. We follow this with results from using simulated data from the Lincoln Laboratory 1999 Intrusion Detection Evaluation study [7], as well as live data monitored in real time from our LAN. Bayesian InferenceMathematically, we have adapted the framework for belief propagation in causal trees from Pearl [
4]. Knowledge is represented as nodes in a tree, where each node is considered to be in one of several discrete states. A node receives![]()
As a consequence of this definition, each row of a CPT is a discrete distribution over the node states for a particular parent node state, that is,
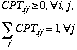
The basic operations of message propagation in the tree are most succinctly expressed in terms of vector/matrix algebra. We will adopt the convention that prior messages are represented as row vectors. Downward propagation of the prior messages is achieved by left multiplication of the parent’s prior by the CPT, that is,
![]()
where
a is a normalizing constant to ensure that the result sums to unity. Note that since CPT is not required to be square, the number of elements in![]()
Note that ![]() has number of elements equal to the number of states in the node, while
has number of elements equal to the number of states in the node, while ![]() has number of elements equal to the number of states in the parent node. These messages are fused at the parent via elementwise multiplication:
has number of elements equal to the number of states in the parent node. These messages are fused at the parent via elementwise multiplication:
![]()
Here, L represents the raw elementwise product, and ![]() is obtained by normalizing this to unit sum. Finally, the belief over the states at a node is obtained as follows:
is obtained by normalizing this to unit sum. Finally, the belief over the states at a node is obtained as follows:
![]()
where
b is a normalizing constant so that BEL has unit sum. Figure 1 illustrates propagation in a fragment of a tree.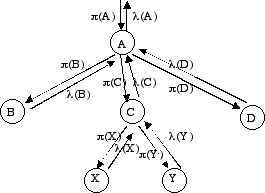
Figure 1: Message Propagation in a Tree Fragment
Session ModelWe evaluate bursts of traffic as a means of integrating the signal (observable evidence of an attack or anomaly). Our simplest model considers temporally contiguous traffic from a particular IP address as a session. To detect distributed attacks, we also consider traffic to a protected resource, such as a server in the protected LAN. When we see an event, we examine our list of active sessions and see if we have a match. If we do, we update the matching session with the new event. Otherwise, we allocate a new session structure and initialize its observables with the event data. We manage the growth of the session list in two ways. First, we have a regularly scheduled "housecleaning" operation. All sessions are allowed to remain active for some time interval after the last event seen for the session. This interval is longer if the system believes the session has open (active) connections, but exists even if all connections are believed to be closed. The timeout intervals for sessions with and without open connections are configuration parameters. When housecleaning is invoked, all sessions for which the timeout is before the time of the housecleaning operation are deallocated. If the session table is at a maximum size set via system configuration and an event for a new session is observed, we invoke a "hindmost" operation, which deallocates the session with the most distant last event time. The inference engine is invoked periodically throughout each session, and always when a session is deallocated.
Identification of when a burst begins or ends is itself not an assertion that can be made with certainty. Even in the case that all connections are closed, we must be careful not to deallocate immediately, as some attacks (such as MAILBOMB) consist of a large number of successful open/close events, any one of which looks normal. Conversely, we must not wait indefinitely (or for the timeout interval) for all open connections to close, as many attacks work by opening connections which the attacker has no intention of completing. Again, a statistical determination of return to the idle state is appropriate, from the point of view of sensitivity as well as response time. The potential downside of deallocating a session prematurely is slight. At worst, we potentially report multiple events for the same attack (although in practice this is rarely seen).
eBayes TCP StructureOur TCP model represents the (unobservable) session class at the root node, and several observed and derived variables from the TCPDUMP data as children. All child nodes are also leaf nodes (that is, considered observable). This structure is represented
Figure 2, and is assumed to hold at each inference interval (or time slice).
Figure 2: eBayes TCP
This structure is sometimes referred to as the naïve Bayes model, and tacitly assumes conditional independence of the child nodes given the parent.
In this model, we apply Bayesian inference to obtain a belief over states of interest (hypotheses) for the session under consideration (or more generally, a burst of traffic from a given IP address). In our TCP model, the session class hypotheses at the root node are MAIL, HTTP, FTP, TELNET/REMOTE USAGE, OTHER NORMAL, HTTP_F, DICTIONARY, PROCESSTABLE, MAILBOMB, PORTSWEEP, IPSWEEP, SYNFLOOD, and OTHER ATTACK. The first five represent normal usage modes, while the rest are attack modes. HTTP_F describes a pattern of long http sessions with abnormal terminations that is frequently seen in real-world traffic. At this point, we do not consider these sessions to represent attacks.
EBayes-TCP is coupled with the eBayes service availability monitor, which learns valid hosts and services in the protected network via a process of unsupervised discovery. This enables detection of "stealth" port sweeps (scanning for a small, sensitive set of ports) without a predefined model of which sets of services are to e considered sensitive.
For each session (as determined by the session model above) we accumulate a number of observables. Inference is done periodically for each session, where the period is a configurable number of events or elapsed time, and always when the system believes the session has ended. The model has three types of measures: intensity, high water marks, and distribution.
Intensity measures are similar to the intensity measures we employed in EMERALD ESTAT. Specifically, an intensity measure is an exponentially decayed count. The intensity measures in eBayes TCP are defined as:

Intensity measures have the property that as long as behavior is normal and the decay constant is appropriately chosen, they do not grow without bound. The range of these measures is categorized to obtain the observed state values for the respective nodes.
High-water-mark measures track a maximum count of an underlying observable. Our system maintains a list of ports and unique hosts accessed by this session. From these, we derive the maximum number of open connections to any unique host. As a configuration option, this maximum may or may not be reset at each inference interval. The total number of unique ports and hosts accessed by the session is also recorded. As with intensity measures, the range is categorized to obtain the respective node states.
Distribution measures track the distribution of the categories over an underlying discrete-valued measure. For example, for each event, we classify the service into one of MAIL, HTTP, FTP, or OTHER. Over an inference interval, we maintain a count of the number of times each was observed. The service distribution is then obtained as
![]()
Strictly, we should divide by the total count to obtain a true distribution, but the normalization in the internals of the Bayes inference handle this for us.
Setting the observables means setting the
l messages at the child nodes. We have overloaded the set_state function to accept either an observed integer state value (in which case we setOur system can potentially adapt by reinforcing its built-in models for the current observation (adjusting rows in the CPTs corresponding to the observed state at the parent) or by adding a new state (hypothesis) at the parent if the current observation is not in good agreement with any of the currently modeled hypotheses.
Adaptive CPT AdjustmentAdaptation via reinforcement proceeds as follows. We recall that the CPT relates a child node to its parent. In our representation, the rows of the CPT correspond to parent states, while the columns correspond to child states. If a single hypothesis is dominant at the root node, we adapt the corresponding row of the CPT matrix at each child slightly in the direction of the
l message at the child node for the present observation. Specifically, if hypothesis![]()
The decayed count is used as a "past weight" for the adjustment, and is the effective number of times this hypothesis has been recently observed. The CPT row is first converted to effective counts for each child state, and the present observation is added as an additional count distributed over the same states. Then the row elements are divided by the row sum so that the adjusted row has unit sum. This is accomplished by the following equation:
![]()
Finally, the internal counts are recomputed for all parent states:
![]()
By this procedure, the effective count never decays below 1.0 (if the hypothesis is never observed) and never grows beyond ![]() if the hypothesis is always observed. We typically choose the decay factor so that the effective count grows to between 200 and 1000 observations. Observations for frequently seen hypotheses have a smaller CPT adjustment than do observations for rare hypotheses. In addition, since only "winning" hypotheses cause a potential CPT adjustment, our system has one key advantage over other statistical ID systems. A large number of observations for a hypothesis corresponding to an attack will not be considered "normal" no matter how frequently it is observed, as its adjustment only reinforces the corresponding internal attack hypothesis model in the system.
if the hypothesis is always observed. We typically choose the decay factor so that the effective count grows to between 200 and 1000 observations. Observations for frequently seen hypotheses have a smaller CPT adjustment than do observations for rare hypotheses. In addition, since only "winning" hypotheses cause a potential CPT adjustment, our system has one key advantage over other statistical ID systems. A large number of observations for a hypothesis corresponding to an attack will not be considered "normal" no matter how frequently it is observed, as its adjustment only reinforces the corresponding internal attack hypothesis model in the system.
Another form of adaptation is the potential ability to add a state. Naïve Bayes models such as the one described above work well in practice as classifiers, and are typically trained with observations for which the true class is known. Dynamic hypothesis generation as described here takes on a more difficult problem, namely, the situation where the data cases are unlabeled and even the underlying number of hypothesis states is unknown. In this situation, it is legitimate to ask if a system can self-organize to a number of hypotheses that adequately separate the important data classes. In this respect, the ability to separate attack classes A and B from each other is less important than the ability to separate both A and B from the set of nonattack classes.
To build this capability, we need to enable the system to add hypotheses at the root node (the reader will recall that the root node state value is not directly observable). As a configuration option, the system will create a "dummy state" at the root node (or more generally, at any node that is not directly observable), with an effective count of 1. If this node has children, a new CPT row is added at each child. We use a uniform distribution over the child state (each element has value ![]() ) for this CPT at present.
) for this CPT at present.
Adding a state then proceeds as follows. The inference mechanism is applied to an observation, and a posterior belief is obtained for the dummy state as if it were a normal state. If this state "wins", it is promoted to the valid state class and the CPT rows for all children are modified via the
CPT adjustment procedure described above. Note that since the effective count of the dummy state is 1, the adjustment makes the CPT rows look 50% like the observation. Then a new dummy state is added, allowing the system to grow to the number of root node states that adequately describe the data. This dummy state is not to be confused with the OTHER ATTACK hypothesis, for which there is an initial model of nonspecific anomalous behavior (e.g., moderate error intensity).There are two ways to exploit the hypothesis generation capability. In the first, we initialize the system with the normal and attack hypotheses
described above, using CPTs derived from our own domain expertise. We observe that the system does adjust the CPTs somewhat, but does not choose to add more hypotheses when running in this fashion. From this, we tentatively conclude that no more than 12 hypotheses are needed to classify these data.Our next experiment examined the other extreme. We initialized the system with a single valid hypothesis and a dummy hypothesis at the root node. We then presented a week of normal (attack-free) data, and the system generated two valid states. As these states were generated, the CPTs were adjusted according to the procedure previously outlined. We then arbitrarily decided that any new states learned would be reported as potential attacks, and presented data known to contain attacks. The system added 2 new states, which captured the attacks seen previously by the 11-state expert-specified model. There were a few false alarms, but well under the Lincoln Laboratory guideline of 10 per day for operational usefulness. Therefore, with the capabilities of adaptation via reinforcement as well as state space expansion described above, it is in fact possible to start the system with essentially no initial knowledge. It then organizes to an appropriate number of hypotheses and CPT values. Interestingly, this system does nearly as well at separating the important classes (here, attack versus nonattack) as the expert-specified model with only 4 root node hypothesis states. Normal data is adequately represented by two states, and the variety of attack data by two abnormal states. While this does tend to separate important normal and attack classes into separate hypotheses, explaining the result is more difficult. Nonetheless, this minimal knowledge approach does remarkably well, and is a very favorable indicator of the generalization potential of our methodology.
In between inference steps, the belief state over session class passes through a Markov transition model, so as to yield a pre-observation belief state immediately before the next inference step. The following sections provide more detailed discussion of the observables used, the state transition, and the Bayes update mechanism.
State TransitionAs a simplifying assumption, the states observed for the respective variables are considered to be independent of what was observed for these variables in past inference intervals, given the session class. In addition, given the value of the session class in the current interval, X is independent of any other observable variable Y. In other words, for all observable variables X, Y and inference intervals 0 to k, we have
![]()
The evolution of session class over inference intervals is modeled as a discrete time-and-state Markov process. The transition matrix is a convex combination of an identity matrix (to express state persistence) and a matrix whose rows are all equal to some prior distribution over the possible values of session class (to express the tendency of the process to decay to some prior state). In other words, for some![]() , the transition matrix M is given by
, the transition matrix M is given by
![]()
where I is an identity matrix and each row of P is given by
![]()
and
PRIOR is a prior distribution over possible values j for session class, that is, ![]()
![]() is the probability that if the process is currently in state
is the probability that if the process is currently in state ![]() it will be in state
it will be in state ![]() at the next event. More generally, if POST_BEL is our current belief state (a distribution over the possible state values, given the evidence up to and including this time interval), left multiplication with M redistributes our belief to obtain the prior belief before the next observation:
at the next event. More generally, if POST_BEL is our current belief state (a distribution over the possible state values, given the evidence up to and including this time interval), left multiplication with M redistributes our belief to obtain the prior belief before the next observation:
![]()
We manipulate the parameter
g to capture, albeit imperfectly, the continuous nature of the underlying process. We typically invoke the inference function every 100 events within a session, and always when the session enters the idle state. Some sessions are less than 100 events in total, while others (particularly many denial-of-service attacks) consist of tens of thousands of events in a very short time interval. In the latter case, even though many inference steps are invoked, we prefer to have a moderately high persistence parameter (about 0.75) because very little time has elapsed. If the parameter is 0, the belief reverts to the prior at each event.It can be shown that, unless ![]() is unity, iteratively multiplying M by itself results in a matrix that approaches P, that is,
is unity, iteratively multiplying M by itself results in a matrix that approaches P, that is,
![]()
In practice, this limit is nearly reached for fairly small values of n. The result of this observation is attractive from the intuitive standpoint: in the absence of reinforcing evidence from subsequent events, the belief distribution tends to revert to the prior.
The inference operation at interval k begins by setting the Bayes ![]() message to
message to ![]() . Then the observables over the interval are presented to the leaf nodes, and the belief state at the root node is extracted. If this is deemed sufficiently suspicious, alert messages are written both to an alert log and in IDIP format.
. Then the observables over the interval are presented to the leaf nodes, and the belief state at the root node is extracted. If this is deemed sufficiently suspicious, alert messages are written both to an alert log and in IDIP format.
Lincoln Laboratory 1999 Evaluation Study
We have run our model against the TCP dump data from the 1999 Lincoln Laboratory IDEVAL data sets [
7]. It is highly effective against floods and nonstealthy probe attacks, and moderately effective against stealthy probe attacks.This data simulates activity at a medium-size LAN with typical firewalls and gateways. Traffic generators simulate typical volume and variety of background traffic, both intra-LAN and across the gateway. Attack scripts of known types are executed at known times, and the traffic (a mix of normal background as well as attack) is collected by standard utilities, such as TCPDUMP.
For this prototype we examined external to internal traffic using the TCP/IP protocol. This means that console attacks, insider attacks, and attacks exploiting other protocols such as IDP and UDP are invisible. These are not theoretical limitations of eBayes, and we intend to include the UDP protocol in the near future. However, this did limit attacks that were visible to the system. The fourth week of the data set was considered the most difficult, as it contained the most stealthy attacks. We detected three visible portsweeps and missed one that accessed 3 ports over 4 minutes with no errors. All of the portsweeps in this data set are stealthy by the standards of the Lincoln training data and the week 5 data (we detect 100% of visible, nonstealthy sweeps). A Satan attack and a TCPRESET attack are also detected as portsweeps. This particular Satan attack was run in a mode where it in fact is characteristic of a portsweep. For the TCPRESET, the portsweep hypothesis slightly edges out the OTHER hypothesis. Other detected attacks in this data include MAILBOMB and PROCESS TABLE (both 100% detected) as well as three password-guessing attacks (one detected as OTHER, two as DICTIONARY). The latter three detections demonstrate the power of the approach. They were not in the set of attacks that Lincoln thought should be detected by this sensor, so we initially considered them false alarms. Further review of the full attack list indicated that they were in fact good detections, even though at that time we had no DICTIONARY hypothesis and they were called OTHER. By elucidating characteristics of these attacks, we added the DICTIONARY hypothesis (indicative of password guessing), which now captures two of these attacks and is a close second to OTHER as a classification for the third. Also, one of these attacks was detected first by probabilistic methods (eStat and later eBayes) because the eXpert sensors had no signature for it. This signature has now been added, but the generalization potential of probabilistic detection is nonetheless clear.
Real-World Experience
We have eBayes-TCP active on our own TCP gateway, and it has proved to be stable for indefinite periods of time. The TCP event generator, EMONTCP, and Bayes inference components require about 15M on a Free BSD platform, and never use more than a few percent of the CPU. For real-world traffic, we of course have no ground truth, but the results have nonetheless proved interesting to us in the sense of scientific experimentation, as well as being of practical interest to our system administrators.
Our initial observation was that, not surprisingly, real-world data contains many failure modes not seen in a set such as the IDEVAL data described above. For example, we regularly observe a pattern of http sessions of moderate or long duration in which a significant number of connections terminate abnormally, but on such a time scale and in such modes that we are fairly certain they are not malicious. To capture these sessions, we decided to add the HTTP_F hypothesis (for failed http). This reduced the alert volume to a manageable 15 or so per day. A representative two-week period comprised about 470,000 connection events, grouped by the session model into about 60,000 sessions of which 222 produced alerts. It is important to point out that many of these are almost certainly attacks, consisting of IP and probe sweeps and some attempted denials of service. Some of the false alert mechanisms are understood and we are actively working to improve system response to these without being too specific (for example, ignoring alerts involving port 113 requests, which are screened in our environment but will be seen from normal mail clients).
The Utility of Learning
The learning procedures described
above have proven useful in our experimentation, guiding us both in refinement of existing hypotheses as well as developing new hypotheses for both normal and attack modalities. However, we have observed better operation if the adaptive capability is disabled, for several reasons. First, attacks and alert-worthy events are a very small fraction of total traffic in a real-world setting, so that learning an attack modality that may only be seen once is problematic. Second, we found that the normal hypotheses become "hardened" so as to be relatively intolerant of erroneous outcomes. The fraction of such outcomes for non-malicious reasons is too high to be tolerable from an alert standpoint, but is too low to permit sufficient "breathing room" if adaptation is permitted indefinitely. For the present, therefore, we run the system in adaptive mode to identify un-anticipated modalities and large CPT deviations from what is observed in true traffic. We then take the results of this phase and moderate it with our judgement (sanding the corners off very hardened hypotheses, so to speak) and arrive at a batch specification of the CPT. We then verify that this new encoding remains sensitive against simulated datasets (such as the Lincoln data). At present, we detect the most attacks we have ever detected in the Lincoln data, and detect alert-worthy events in our real-world data with an acceptable level of apparent false alerts.Summary
We have described the eBayes monitoring capability, which employs Bayesian inference steps with transition models between inference to assess whether a particular burst of traffic contains an attack. A coupled component monitors availability of valid services, which are themselves learned via unsupervised discovery.
The efficacy of this system was demonstrated by results from the Lincoln Laboratory Intrusion Detection Evaluation data, and also by a live operation on a real-world site for weeks at a time.
This provides us with several important new capabilities:
We continuously run this system along with our TCP session monitor on our own TCP gateway. While we do not have ground truth for this traffic, we regularly identify probe attacks and "spidering" activity, as well as the occasional DOS attempt. We also detect service outages and recovery for what appear to be nonmalicious faults.
Acknowledgements
This research was sponsored by DARPA under contract number F30602-99-C-1049. The views herein are those of the author(s) and do not necessarily reflect the views of the supporting agency.
References